1、连续可导与积分的关系1一致连续性定理 若函数fx在闭区间a,b 上连续,则fx在闭区间 a,b 上一致连续2 可积的条件 1可积的必要条件 定理 若函数fx在 a,b 上可积,则fx在 a,b 上必有界2可积的充分条件 定理1 若函数fx在 a。
2、1,一元函数可导必然连续,连续推不出可导,可导与可微等价2,多元函数可偏导与连续之间没有联系,也就是说可偏导推不出连续,连续推不出可偏导3,多元函数中可微必可偏导,可微必连续,可偏导推不出可微,但若一阶偏导具有连续性则可推出可微4,对于多元函数来说某点处偏导数存在与。
3、可导函数一定连续,这是因为可导性蕴含了连续性的必要条件以下是通俗解释导数的极限定义若函数在某点可导,意味着该点的导数存在导数是通过极限来定义的,具体为一个分式,其中分母为无穷小量分子也为无穷小由于分母趋向于0,为了保证导数存在,分子也必须趋向于0这意味着函数值在该点附近。
4、首先在闭区间上连续是为了使用费马引理其次在一点可导的一般情况,是左右导数都存在并且相等所以如果将在开区间可导换为在闭区间可导,则对于端点处,可导性就成了左可导和右可导,这只是可导的特例,而作为定理,我们需要描述的是一般情况,因此用开区间罗尔定理微分中值定理广义微分中值定理即。

5、可导的函数一定要连续,原因在于可导性建立在连续性的基础上以下是具体原因连续性的基础作用连续性描述了函数在某个点或区间上的稳定性和一致性它确保了函数在该点的取值与附近取值的连贯性,即函数图象在该点平滑且无突变可导性的定义可导性关注函数在该点或区间内的变化率,即瞬时变化率。
6、函数一定要连续才可导,是因为连续性是函数在某一点可导的必要条件以下是具体解释连续性的定义函数在某一点连续意味着在该点处的函数极限存在且等于函数在该点的值这是函数在该点行为稳定的一种表现可导性的定义函数在某一点可导,意味着在该点处函数有一个确定的斜率,即函数在该点的导数。
7、这正好符合连续函数的定义,说明函数在\x_1\处连续因此,我们得出如果一个函数在一个区间上可导,那么它的导函数在这个区间上一定是连续的这个结论在高等数学中被广泛使用,并且是许多定理的基础值得注意的是,这个结论只适用于一元函数对于二元函数,情况可能会有所不同,可导性与连续性的。
8、因为如果这个函数前提是连续的设fx=x这个函数连续,到时在x=0的时候fx不可导,这就是连续不一定可导连续的定义1点函数值等于该点极限2该点有定义3函数有极限可导要满足1导数存在2左右导数相等比如说y= x这个函数就不满足上述所说的可导性,因为在x =。
9、可导函数一定连续,原因如下导数存在的前提导数存在的前提条件是,当自变量的微小变化趋于零时,对应的函数值变化与自变量变化之比的极限存在这实际上已经蕴含了函数在该点的连续性,因为只有当函数值的变化也趋向于零时,这个比值才可能存在极限连续性的定义函数连续的定义是,当自变量变化趋向于。
10、可导函数一定连续,原因如下导数存在的前提导数存在的前提条件是,当自变量的微小变化趋于零时,对应的函数值变化与自变量变化之比的极限存在这实际上已经蕴含了函数在该点的连续性,因为只有当函数值的变化也趋向于零时,这个比值才可能存在极限连续性的定义函数连续的定义是,当自变量变化趋向于某点时,函数值也趋近于该点处的。
11、可导必连续,意思是一个函数可导,则导函数存在,不能说明导函数的极限存在,也不能说明导函数连续导函数简介如果函数fx在a,b中每一点处都可导,则称fx在a,b上可导,则可建立fx的导函数,简称导数,记为f#39x如果fx在a,b内可导,且在区间端点a处的右导数和端点。
12、可导不一定是连续的可导函数的导函数不一定连续,可以有震荡间断点,例如把ft=sin1t*t^2的可去间断点t=0补充定义f0=0,得到的新函数可导,导函数在t=0处间断连续不一定可导所以,左右导数存在且相等就能保证该点是连续的导数的起源 导数起源大约在1629年,法国数学家费马研究了。
13、函数的连续性和可导性是微积分中两个基本且紧密关联的概念可导性意味着函数在某点的切线存在且唯一,因此,它在该点处的极限必须存在且左右极限相等这个条件不仅保证了函数在该点有定义,还意味着函数在该点连续所以,可导一定意味着连续然而,连续性并不自动意味着可导性连续性意味着函数在某。
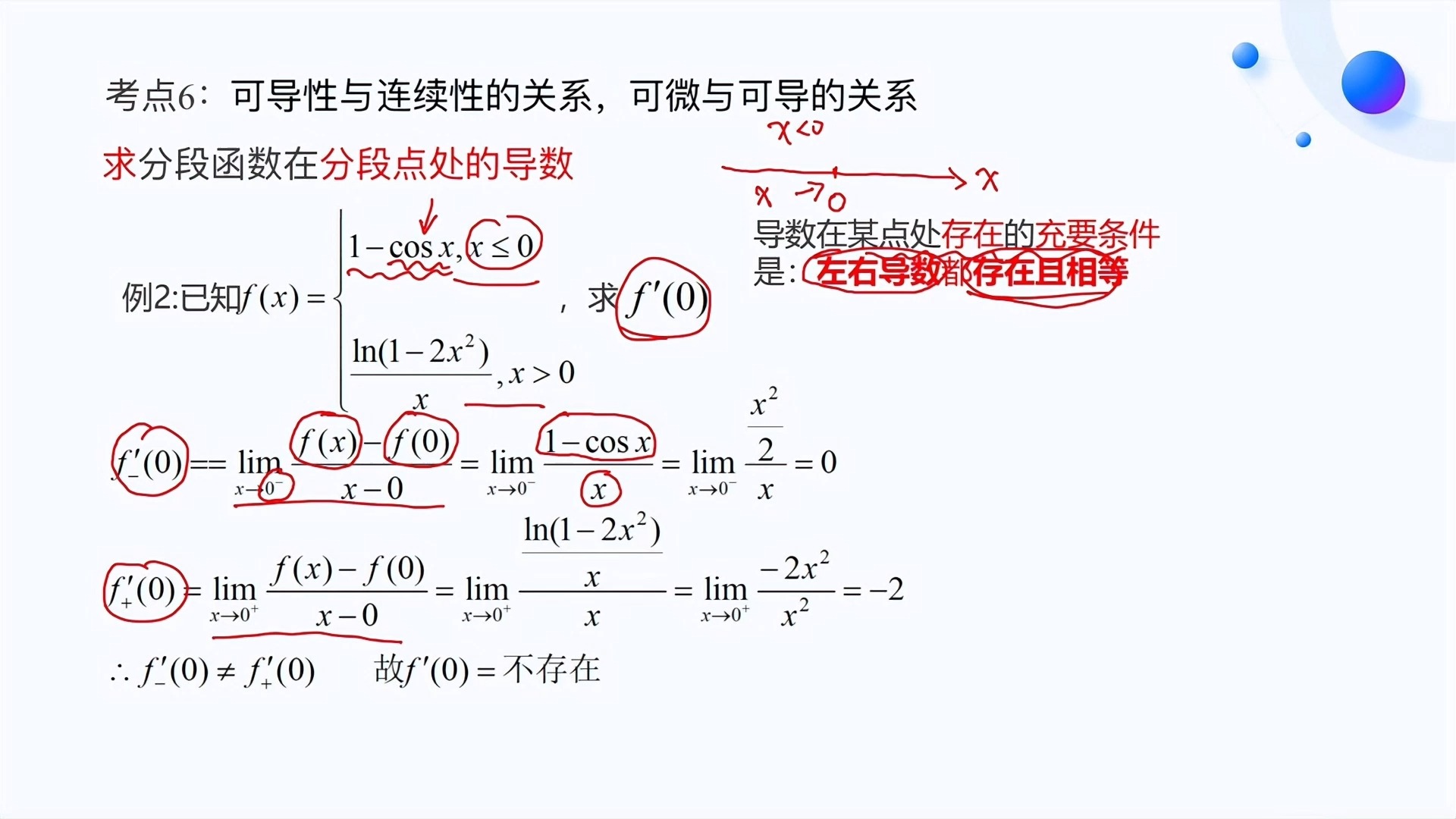
14、可微与连续的关系可微与可导是一样的可积与连续的关系可积不一定连续,连续必定可积可导与可积的关系可导一般可积,可积推不出一定可导可导,即设y=fx是一个单变量函数, 如果y在x=x0处左右导数分别存在且相等,则称y在x=x0处可导如果一个函数在x0处可导,那么它一定在x。
15、2可导是可微的必要条件对于多元函数,如果函数在某一点处可导,则该点处一定可微这是因为多元函数的可导性需要偏导数存在且连续,而偏导数就是函数在该点处的变化率,因此它们之间存在一一对应关系3可微是可导的充分条件对于一元函数,如果函数在某一点处可微,则该点处一定可导这是因为一元。


