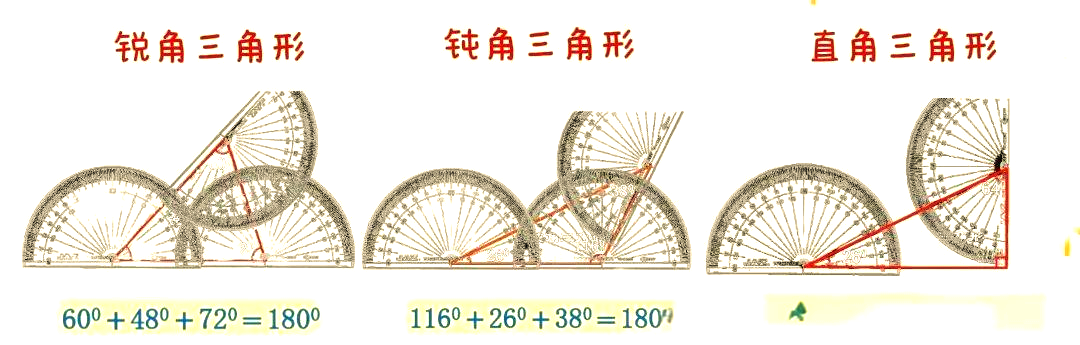
将三个一样大小的三角形在三个对应角的位置上,分别标上三个字母A,B,C然后将第一个三角形的A角,第二个三角形的B角,第三个三角形的C角,拼在一起,这时它们的下边或上边就正好形成一条直线即三个角形成了一个平角,就是说三个角的度数和是一百八十度而这三个角是三角形的三个内角。
三角形的内角和之所以是180度,主要有以下原因一几何折叠法 通过将三角形的三个角分别向内折叠,可以发现这三个角恰好能组成一个平角,即180度这种方法直观且易于理解,是证明三角形内角和为180度的一种简单方式二邻补角与外角关系 延长三角形的一条边,可以形成一个三角形的外角这个外角。

三角形内角和不一定是180度如下在同一个平面内,三角形内角的和一定是180°但不在同一个平面内,三角形的内角和可能大于180°,也可能小于180°有数学家提出在同一个平面内,三角形内角的和不一定是180°但是这个理论比较难理解,还没有得到多数人的认可。
由此可知,通过平移,可将三角形内角排列成一条直线,构成180度另一种思路是考虑外角,所有外角加和为360度内外角和为180度,因此三个平角减去一个周角后,剩余一个平角这一结论完全依赖于角的平移及不变性质在非欧式几何中,即便直线平行无法保证,或无法平移角,三角形内角和的180度结论自然。
三角形内角和为180°,这其实是平面几何的必然结果,也是几何原本中第五公设的推论如果离开了平面几何,比如在一些曲面上,三角形的内角和是可以不等于180°的我们有很多方法,来证明平面内三角形内角和为180°,也就是一个平角的角度,但是无论我们用到什么方法,本质上都用到了欧几里得第五。
三角形的内角和为180度的原因主要有以下几点图形拼接法将三个大小相同的三角形在对应角的位置上分别标上ABC将第一个三角形的A角第二个三角形的B角第三个三角形的C角拼在一起,它们会形成一个平角平角的度数为180度,因此三角形的三个内角和为180度平行线性质法对于任意三角。
三角形的内角和是180度的原因主要有以下几点几何折叠法将三角形的三个角分别向内折叠,它们会组成一个平角,即180度邻补角与平行线性质延长三角形的一条边,形成三角形的外交该外交与相邻的内角之和为180度,即它们是邻补角过这个内角的顶点作一条直线,平行于这个角的对边,将外交分成两。


